Question

ITS TIMED PLEASE HELP​

Answer 1

The graph of the function
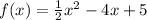`f(x)=(1)/(2)x^(2)-4x+5` has a minimum located at (4,-3)

Explanation:

we know that

The equation of a vertical parabola in vertex form is equal to

`f(x)=a(x-h)^(2)+k`

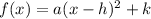
where

a is a coefficient

(h,k) is the vertex of the parabola

If a > 0 the parabola open upward and the vertex is a minimum

If a < 0 the parabola open downward and the vertex is a maximum

In this problem

The coefficient a must be positive, because we need to find a minimum

therefore

Check the option C and the option D

Option C

we have

`f(x)=(1)/(2)x^(2)-4x+5`

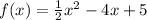
Convert to vertex form

`f(x)-5=(1)/(2)x^(2)-4x`

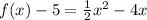
Factor the leading coefficient

`f(x)-5=(1)/(2)(x^(2)-8x)`

`f(x)-5+8=(1)/(2)(x^(2)-8x+16)`

`f(x)+3=(1)/(2)(x^(2)-8x+16)`

`f(x)+3=(1)/(2)(x-4)^(2)`

`f(x)=(1)/(2)(x-4)^(2)-3`

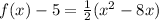
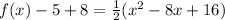
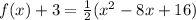
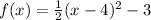
The vertex is the point (4,-3) ( is a minimum)

therefore

The graph of the function
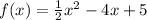`f(x)=(1)/(2)x^(2)-4x+5` has a minimum located at (4,-3)