Question

Billy is helping to make pizzas for a school function. He's made 25 pizzas so far. His principal asked him to make at least 30 pizzas but no more than 75. Solve the compound inequality and interpret the solution.

30 ≤ x + 25 ≤ 75

5 ≥ x ≥ 50; Billy needs to make less than 5 more pizzas or more than 50.
5 ≤ x ≤ 50; Billy needs to make at least 5 more pizzas but no more than 50.
55 ≤ x ≤ 100; Billy needs to make at least 55 more pizzas but no more than 100.
55 ≥ x ≥ 100; Billy needs to make less than 55 more pizzas or more than 100.

Answer 1

Answer: 5 ≤ x ≤ 50; Billy needs to make at least 5 more pizzas but no more than 50.

Explanation:

Given : Billy is helping to make pizzas for a school function. He's made 25 pizzas so far. His principal asked him to make at least 30 pizzas but no more than 75.

Let x be the number of pizzas Billy needed to make.

The compound inequality for the given situation is :
`30\leq x + 25 \leq 75`

To solve the given inequality , we subtract 25 on the each side, we get

`30-25 \leq x \leq75-25\\\\\Rightarrow\ 5\leq x\leq 50`

It means that Billy needs to make at least 5 more pizzas but no more than 50.

Answer 2

5 ≤ x ≤ 50; Billy needs to make at least 5 more pizzas but no more than 50

Explanation:

Let

x -----> the number of pizzas

we have the compound inequality

`30 \leq x+25 \leq 75`

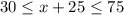
Divide the compound inequality into two inequalities

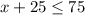`x+25 \leq 75` ----> inequality A

`x \leq 75-25`

`x \leq 50\ pizzas`

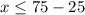
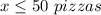
The solution of the inequality A is the interval -----> (-∞,50]

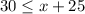`30 \leq x+25` -----> inequality B

`30-25 \leq x`

`5 \leq x`

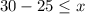
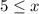
Rewrite

`x \geq 5`

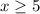
The solution of the inequality B is the interval -----> [5,∞)

therefore

The solution of the compound inequality is

(-∞,50] ∩ [5,∞)=[5,50]

so

`5\leq x \leq 50`

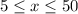
Billy needs to make at least 5 more pizzas but no more than 50