Question

Please help me out!​

Answer 1

Second option

Third option

Fourth option

Explanation:

We have the following quadratic function

`f(x) =(x-1)(x+7)`

Use the distributive property to multiply the expression

`f(x) =x^2+7x-x-7`

`f(x) =x^2+6x-7`

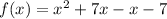
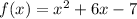
For a function of the form
`f (x) = ax ^ 2 + bx + c` the x coordinate of the vertex is:

`x =-(b)/(2a)`

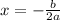
Then in this case the coordinate of the vertex is:

`x =-(6)/(2(1))`

`x =-3`

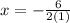
To obtain the y coordinate of the vertex we evaluate the function at
`x = -3`

`f(-3) =(-3)^2+6(-3)-7`

`f(-3) =9-18-7`

`f(-3) =-16`

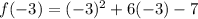
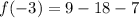
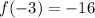
Then the vertex is: (-3, -16)

We can see in the graph that the zeros of the function are x=1 and x=-7

Then the function is decreasing from -∞ to -3 and then it is increasing from -3 to ∞

The function is positive for
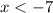`x <-7` and
`x> 1`

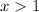
The correct answers are:

Second option

Third option

Fourth option