Answer:
6.78 m/s
Step-by-step explanation:
Let the distance between the two friends is x .
Radius, r = 120 m
v = 7 m/s
Angular velocity, ω = v / r = 7 / 120 rad/s
Use the law of cosines for the triangle OAB
x^2 = 120^2 + 240^2 - 2 x 120 x 240 x Cosθ ...... (1)
differentiate with respect to t on both the sides
2 x dx/dt = - 57600 x (-Sinθ) dθ/dt
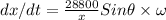 . ........ (2)
. ........ (2)
Put x = 240 m in equation (1), we get
240^2 = 120^2 + 24062 - 57600 Cosθ
Cosθ = 1/4
So, by the use of right angled triangle, Sinθ = √15/4
Put all the values in equation (2), we get
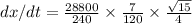
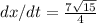 m/s = 6.78 m/s
m/s = 6.78 m/s