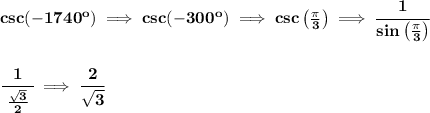Question

Find the exact value of csc(-1740)degrees

Answer 1

let's recall that negative angles go clockwise, so we have -1740°, how many revolutions is that? 1740 - 360 - 360 - 360 - 360 = 300, meaning, that 360 + 360 + 360 + 360 + 300 = 1740.

So, if we move clockwise and go around 4 times over, and then land on -300°, we'll be landing on the 1st Quadrant as you see in the picture below.

`\bf csc(-1740^o)\implies csc(-300^o)\implies csc\left( (\pi )/(3) \right)\implies \cfrac{1}{sin\left( (\pi )/(3) \right)} \\\\\\ \cfrac{~~1~~}{(√(3))/(2)}\implies \cfrac{2}{√(3)}`

Answer 2

`(2)/(√(3))`

Explanation:

Consider
`\csc (-1740^(\circ))`

We know that angle
`-\theta` lies in fourth quadrant and
`\csc(-\theta )` is negative in the fourth quadrant .

So,
`\csc (-1740^(\circ))=-\csc(1740^(\circ) )`

We can write
`1740^(\circ)` as
`1740^(\circ)=10\pi-60^(\circ)`

Therefore,

`\csc (-1740^(\circ))=-\csc(1740^(\circ) )=-\csc\left ( 10\pi-60^(\circ) \right )\\\csc(-\theta )`

Here,
`10\pi-60^(\circ)` lies in fourth quadrant in which cosec function is negative, so
`\csc (-1740^(\circ))=-\csc(1740^(\circ) )=-\csc\left ( 10\pi-60^(\circ) \right )\\\csc(\theta )=\csc \left ( 60^(\circ) \right )=(2)/(√(3))`