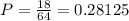Question

Suppose we write the numbers $1,2,3,4,5,6$, and then color each number red or blue. The coloring is called factorific if there is at least one blue number, and for each blue number, all of its divisors are also blue. Grogg randomly colors some, all, or none of the numbers from 1 to 6 blue, and he colors the rest red. What is the probability that his coloring is factorific?

Answer 1

The probability that his coloring is factorific is 0.28125

Explanation:

For calculate the probability is necessary to identify the total number of ways to color the six number. This can be calculate with the rule of multiplication as:

2*2*2*2*2*2=64

Because we have 2 options to color every number.

For know the number of ways in which the coloring is factorific, first we need to identify the divisors of each number:

1: the divisor is 1

2: The divisors are 2 and 1

3: The divisors are 3 and 1

4: The divisors are 4, 2 and 1

5: The divisors are 5 and 1

6: The divisors are 6, 3 and 1

From these information we analyse that for made a factorific coloring, is necessary that the number 1 is color blue. Additionally if the number 4 is color blue, the number 2 needs to be color blue and if the number 6 is blue, the number 3 needs to be blue.

So, the number of ways in which we can create a factorfic number is determined by the following cases:

• The number 2 is blue and the number 3 is blue: In this case we have 1 option for number 1, one for number 2 and 1 for number 3. Taking into account that the number 2 and 3 are blue, if the number 4 and 6 are blue or red doesn't change the fact that the coloring is going to be factorific. So, we have two options for number 3 and 2 options for number 6. Finally the color of the number 5 is independent of the colors of number 2 and 3, so we also have 2 options for coloring number 5 and the coloring is going to be factorific. Then the number of ways for this situation is calculate as:

1 * 1 * 1 * 2 * 2 * 2 = 8

number 1 number 2 number 3 number 4 number 5 number 6

At the same way we can calculate the following cases:

• The number 2 is blue and the number 3 is red: If the number 3 is red, the coloring is only going to be factorific is number 6 is red. Then the number of ways for this situation is calculate as:

1 * 1 * 1 * 2 * 2 * 1 = 4

number 1 number 2 number 3 number 4 number 5 number 6

• The number 2 is red and the number 3 is red: If the number 2 and 3 are red, the coloring is only going to be factorific is number 4 and 6 are red. Then the number of ways for this situation is calculate as:

1 * 1 * 1 * 1 * 2 * 1 = 2

number 1 number 2 number 3 number 4 number 5 number 6

• The number 2 is red and the number 3 is blue: If the number 2 is red, the coloring is only going to be factorific is number 4 is red. Then the number of ways for this situation is calculate as:

1 * 1 * 1 * 1 * 2 * 2 = 4

number 1 number 2 number 3 number 4 number 5 number 6

If we sum all the cases, we obtain 18 ways to make a factorific coloring. So the probability can be calculated as:

`P= (18)/(64) =  0.28125`