Question

Two cars have identical horns, each emitting a frequency of fs = 395 Hz. One of the cars is moving with a speed of 12.0 m/s toward a bystander waiting at a corner, and the other car is parked. The speed of sound is 343 m/s. What is the beat frequency heard by the bystander?

Answer 1

The beat frequency heard by the bystander is 14.32 Hz

Step-by-step explanation:

Given that,

Emitting frequency = 395 Hz

Speed of cars = 12.0 m/s

Speed of sound = 343 m/s

We need to calculate the frequency

Using formula of frequency

`f=\dfrc{v}{v'-v}* f_(0)`

Where, v = speed of sound

v' = speed of cars

f₀= emitting frequency

Put the value into the formula

`f=(343)/(343-12)*395`

`f=409.32\ Hz`

We need to calculate the beat frequency heard by the bystander

`f'=f-f_(0)`

`f'=409.32-395`

`f'=14.32\ Hz`

Hence, The beat frequency heard by the bystander is 14.32 Hz.

Answer 2

14.32 Hz

Step-by-step explanation:

Given:

Frequency of the horn, f₀ = 395 Hz

Speed of the car, v = 12.0 m/s

Speed of the sound, c = 343 m/s

now, applying the doppler's effect formula, we have

`f=f_0((c)/(c-v))`

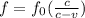
where,

f is the observed frequency

on substituting the values, we get

`f=395*((343)/(343-12))`

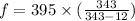
or

f = 409.32 Hz

therefore,

the beat frequency heard is = f - f₀ = 409.32 - 395 = 14.32 Hz