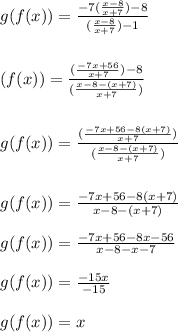Question

Confirm that f and g are inverses by showing that f(g(x)) = x and g(f(x)) = x. f(x) = quantity x minus eight divided by quantity x plus seven and g(x) = quantity negative seven x minus eight divided by quantity x minus one.

Answer 1

the top person is correct

Explanation:

Answer 2

`g(f(x))=(-7((x-8)/(x+7))-8)/(((x-8)/(x+7))-1)\\\\g(f(x))=x`

`f(g(x))=(((-7x-8)/(x-1))-8)/(((-7x-8)/(x-1))+7)\\\\\\f(g(x))=x`

Explanation:

First we write the function f(x)

`f(x) = (x-8)/(x+7)`

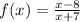
Now we write the function g(x)

`g(x)=(-7x-8)/(x-1)`

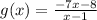
First we find
`f (g (x))`

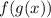
To find
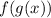`f(g(x))` you must enter the function g(x) into the function f(x) by making
`x = g (x)`

`f(g(x))=(((-7x-8)/(x-1))-8)/(((-7x-8)/(x-1))+7)`

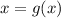
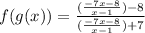
Now we simplify the expression

`f(g(x))=(((-7x-8)/(x-1))-8)/(((-7x-8)/(x-1))+7)\\\\\\f(g(x))=(((-7x-8-8(x-1))/(x-1)))/(((-7x-8+7(x-1))/(x-1)))\\\\\\f(g(x))=(-7x-8-8(x-1))/(-7x-8+7(x-1))\\\\\\f(g(x))=(-7x-8-8x+8)/(-7x-8+7x-7)\\\\\\f(g(x))=(-15x)/(-15)\\\\\\f(g(x))=x`

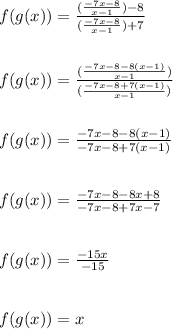
Now we find
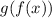`g(f(x))` doing
`x = f (x)`

`g(f(x))=(-7((x-8)/(x+7))-8)/(((x-8)/(x+7))-1)`

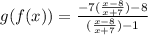
Now we simplify the expression

`g(f(x))=(-7((x-8)/(x+7))-8)/(((x-8)/(x+7))-1)\\\\\\\g(f(x))=(((-7x+56)/(x+7))-8)/(((x-8-(x+7))/(x+7)))\\\\\\g(f(x))=(((-7x+56-8(x+7))/(x+7)))/(((x-8-(x+7))/(x+7)))\\\\\\g(f(x))=(-7x+56-8(x+7))/(x-8-(x+7))\\\\g(f(x))=(-7x+56-8x-56)/(x-8-x-7)\\\\g(f(x))=(-15x)/(-15)\\\\g(f(x))=x`