Question

A 8.61-cm long solenoid consists of 677 turns of a 1.46-cm diameter circular coil. The total resistance of the coil is 0.684 \OmegaΩ. Calculate the energy stored in the magnetic field of the solenoid when 0.728 Volts is applied across the solenoid leads. Give your answer in units of milliJoules.

Answer 1

The energy stored in the magnetic field of the solenoid is 0.633 mJ.

Step-by-step explanation:

Given that,

Length = 8.61 cm

Number of turns = 677

Diameter = 1.46 cm

Resistance = 0.684 Ω

emf = 0.728 V

We need to calculate the energy stored in the magnetic field

Using formula of inductance

`L=(\mu_(0)N^2A)/(l)`

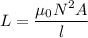
Where, N = number of turns

A= area

I = Current

Put the value into the formula

`L=(4\pi*10^(-7)*677^2*\pi(*0.73*10^(-2))^2)/(8.61*10^(-2))`

`L=1.119*10^(-3)\ H`

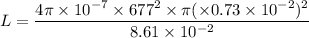
We need to calculate the current

Using ohm's law

`I=(V)/(R)`

`I=(0.728)/(0.684)`

`I=1.064\ A`

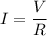
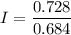
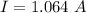
We need to calculate the stored energy

Using formula of store energy

`E=(1)/(2)LI^2`

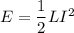
Put the value into the formula

`E=(1)/(2)*1.119*10^(-3)*(1.064)^2`

`E=0.633*10^(-3)\ J`

`E=0.633\ mJ`

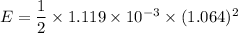
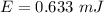
Hence, The energy stored in the magnetic field of the solenoid is 0.633 mJ.