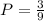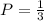Answer: Option C
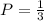
Explanation:
We have a three section spinner and we want to know what is the probability of spinning the spinner twice and getting the same number.
The tree diagram shows that by spinning the spinner 2 times there are 9 possible results
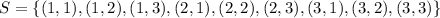
Note that among these 9 possible outcomes there are 3 ways to get the same number
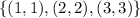
Then the definition of probability tells us that:

In this case

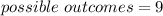
Finally