Answer:
The inequality is:

which can be simplified into:

Step-by-step explanation:
Assume the following:
s is the number of days Darcie can skip crocheting
t is the total number of days left before donation = 60 days
r is the number of days required to crochet 3 blankets
Now, for the given problem:
We are given that Darcie crochets at a rate of 1/15 of a blanket per day
We start by getting the number of days required to crochet 3 blankets
Number of day required =
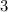 ÷
÷
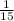
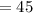 days
days
The number of days Darcie can skip must be less than or equal to the difference between the total number of days left and the number of days required to crochet the 3 blankets
s ≤ t - r
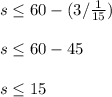
The above inequality means that Darcie can crocheting at most 15 days in order to be able to meet her target
Hope this helps :)