Question

What is the radical expression that is equivalent 27 1/5?

Enter your answer as a radical. For example, if your answer is 3√14, enter your answer like this: cuberoot(14)

Answer 1

The required expression is
`27^{(1)/(5) } = \sqrt[5]{27}` or
`27^{(1)/(5) } = \sqrt[5]{3^3}`

Explanation:

Consider the provided expression :
`27^{((1)/(5) )}`

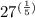
We need to find the radical expression.

Use the property:

`\sqrt[n]{x} = x^(1)/(n)`

Where n is the index of the radical.

By using the above property we can rewrite the above expression as:

`27^{(1)/(5) } = \sqrt[5]{27}`

OR

We can write 27 = 3×3×3 = 3³

`\sqrt[5]{27} = \sqrt[5]{3^3}`

Therefore, the required expression is
`27^{(1)/(5) } = \sqrt[5]{27}` or
`27^{(1)/(5) } = \sqrt[5]{3^3}`

Answer 2

For this case we have to define properties of powers and roots that:

`\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}`

So, if we have the following expression:

`27 ^ {\frac {1} {5}}`

We can rewrite it as:

`\sqrt [5] {27 ^ 1} = \sqrt [5] {27}`

ANswer:

`\sqrt [5] {27}`