Answer:
The required expression is
![27^{(1)/(5) } = \sqrt[5]{27}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/27mnqsjrqbfabwrfxcocc2o87bw424zut3.png) or
or
![27^{(1)/(5) } = \sqrt[5]{3^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kh8wlptgtw70wreh8sp40n9g251eqv1dl8.png)
Explanation:
Consider the provided expression :
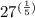
We need to find the radical expression.
Use the property:
![\sqrt[n]{x} = x^(1)/(n)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/elk77odg24qbq66mxtttax1zdcbbrrb3kr.png)
Where n is the index of the radical.
By using the above property we can rewrite the above expression as:
![27^{(1)/(5) } = \sqrt[5]{27}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/27mnqsjrqbfabwrfxcocc2o87bw424zut3.png)
OR
We can write 27 = 3×3×3 = 3³
![\sqrt[5]{27} = \sqrt[5]{3^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dax8bynmjxt4gyjsrha4dr6nnroujkta0a.png)
Therefore, the required expression is
![27^{(1)/(5) } = \sqrt[5]{27}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/27mnqsjrqbfabwrfxcocc2o87bw424zut3.png) or
or
![27^{(1)/(5) } = \sqrt[5]{3^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kh8wlptgtw70wreh8sp40n9g251eqv1dl8.png)