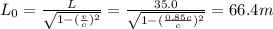Question

A rocket passes you at a speed of 0.85c, and you measure its length to be 35.0 m. What is its measured length when at rest?

Answer 1

66.4 m

Step-by-step explanation:

To solve the problem, we can use the length contraction formula, which states that the length observed in the reference frame moving with the object (the rocket) is given by

`L=L_0 \sqrt{1-((v)/(c))^2}`

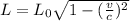
where

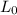`L_0` is the proper length (the length measured from an observer at rest)

v is the speed of the object (the rocket)

c is the speed of light

Here we know

v = 0.85c

L = 35.0 m

So we can re-arrange the equation to find the length of the rocket at rest:

`L_0 = \frac{L}{\sqrt{1-((v)/(c))^2}}=\frac{35.0}{\sqrt{1-((0.85c)/(c))^2}}=66.4 m`