Explanation:
a)
First, when simplifying radicals, we prime factorize the number within the radical. In this case, it's
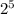 . For square roots, when we have 2 of the same prime number, it goes outside the radical. However, when it goes outside the radical, we only write that number once.
. For square roots, when we have 2 of the same prime number, it goes outside the radical. However, when it goes outside the radical, we only write that number once.
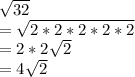
b)
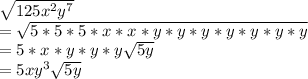
c)
For this, we want the cubic root, so we need at least 3 of a number for it to go outside the radical.
![\sqrt[3]{24x^(3)y^(8) } \\=\sqrt[3]{2*2*2*3*x*x*x*y*y*y*y*y*y*y*y} \\=2*x*y*y\sqrt[3]{3*y*y} \\=2xy^(2) \sqrt[3]{3y^(2) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/3rybbuna1kbg4yrrxf27p2pqoxyq7lkxnr.png)