Question

Just before a referendum on a school​ budget, a local newspaper polls 402 voters to predict whether the budget will pass. Suppose the budget has the support of 52​% of the voters. What is the probability that the​ newspaper's sample will lead it to predict​ defeat?

Answer 1

21.21%

Explanation:

Assume that proportion of support follows normal distribution.For resulting in defeat the proportion of support should less than 0.5.Given that the proportion of support is p= 0.52.

Sample size(n)= 402

We know that standard deviation is given as

`\sigma = \sqrt {\frac {p(1-p)}{n}}`

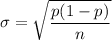
Now by putting the values

`\sigma = \sqrt {(0.52* 0.48)/(402)}`

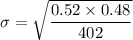
σ=0.0249

Proportion of support follows normal distribution with mean is 0.52 and standard deviation is 0.0249

We know that
`Z=\frac{\bar{X}-\mu }{\sigma }`

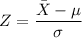
So

`Z=(0.5-0.52 )/(0.0249)`

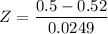
Z= -0.80

So P(Z<-.80) =0.2118 from standard table.

So the probability of news paper to predict defeat is 21.21%