Question

If f(x) = 2x2 +5/(x-2), complete the following statement:

The domain for (x) is all real numbers ___ than or equal to 2.
Answer here

Answer 1

For this case we have the following function:

`f (x) = 2x ^ 2 + \frac {5} {x-2}`

By definition, we have that the domain of a function is given by all the values for which the function is defined. The given function is not defined when the denominator is zero.

So:

`x-2 = 0\\x = 2`

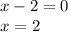
Thus, the function is not defined at
`x = 2.`

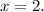
The domain is given by all real numbers except 2.

Answer:

The domain is given by all real numbers except 2.