Question

What is the lateral area of a regular square pyramid if the base edges are of length 24 and perpendicular height is 5?

Answer 1

The lateral area is 624 unit²

Explanation:

* Lets explain how to solve the problem

- The regular square pyramid has a square base and four congruent

triangles

- The slant height of it =
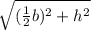`\sqrt{((1)/(2)b)^(2)+h^(2)}`, where

b is the length of its base and h is the perpendicular height

- Its lateral area =
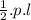`(1)/(2).p.l`, p is the perimeter of the base

and l is the slant height

* Lets solve the problem

∵ The base of the pyramid is a square with side length 24 units

∵ Its perpendicular height is 5 units

∵ The slant height (l) =
`\sqrt{((1)/(2)b)^(2)+h^(2)}`

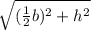
∴ l = The slant height of it =
`\sqrt{((1)/(2).24)^(2)+5^(2)}`

∴ l =
`\sqrt{(12)^(2)+25}=√(144+25)=√(169)=13`

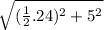
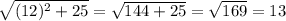
∴ l = 13 units

∵ Perimeter of the square = b × 4

∴ The perimeter of the base (p) = 24 × 4 = 96 units

∵ The lateral area =
`(1)/(2).p.l`

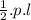
∴ The lateral area =
`(1)/(2).(96).(13)`

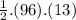
∴ The lateral area = 624 unit²

* The lateral area is 624 unit²