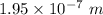Question

A transparent oil with index of refraction 1.28 spills on the surface of water (index of refraction 1.33), producing a maximum of reflection with normally incident green light (wavelength 500 nm in air). Assuming the maximum occurs in the first order, determine the thickness of the oil slick.

Answer 1

The thickness of the oil slick is
`1.95*10^(-7)\ m`

Step-by-step explanation:

Given that,

Index of refraction = 1.28

Wave length = 500 nm

Order m = 1

We need to calculate the thickness of oil slick

Using formula of thickness

`2nt= m\lambda`

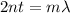
Where, n = Index of refraction

t = thickness

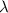`\lambda` = wavelength

Put the value into the formula

`2*1.28 * t=1**500*10^(-9)`

`t = (1**500*10^(-9))/(2*1.28 )`

`t=1.95*10^(-7)\ m`

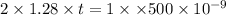
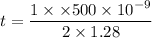
Hence, The thickness of the oil slick is
`1.95*10^(-7)\ m`