The fundamental frequency on a vibrating string is given by:
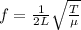
where
L is the length of the string
T is the tension
 is the mass per unit length of the string
is the mass per unit length of the string
Keeping this equation in mind, we can now answer the various parts of the question:
(a) The fundamental frequency will halve
In this case, the length of the string is doubled:
L' = 2L
Substituting into the expression of the fundamental frequency, we find the new frequency:
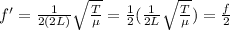
So, the fundamental frequency will halve.
(b) the fundamental frequency will decrease by a factor

In this case, the mass per unit length is doubled:
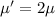
Substituting into the expression of the fundamental frequency, we find the new frequency:
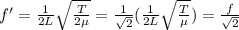
So, the fundamental frequency will decrease by a factor
 .
.
(c) the fundamental frequency will increase by a factor

In this case, the tension is doubled:
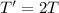
Substituting into the expression of the fundamental frequency, we find the new frequency:
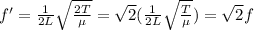
So, the fundamental frequency will increase by a factor
 .
.