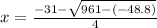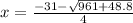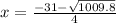Answer:
Using the quadratic formula
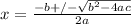
The answer to the equation
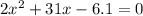 using at least three significant figures is:
using at least three significant figures is:
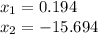
Explanation:
The quadratic formula is used to solve polynomials of second degree.
We have a polynomial of second degree to be resolved with the quadratic formula:
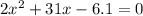 (Eq. 1)
(Eq. 1)
We know the quadratic formula is:
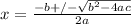 (Eq. 2)
(Eq. 2)
To resolve the quadratic formula we need the a, b and c coefficients, we can find these coefficients in the equation 1.
a: Coefficient that accompanies

b: Coefficient that accompanies

c: Independent term
With this information and the equation (1). We know the values of a, b and c
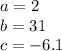
Now, we can replace these terms in the quadratic formula (Eq. 2)
The first root will be found using the positive sign before the square root:
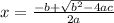
![x=\frac{-31+\sqrt{31^(2)-[4*2*(-6.1)]} }{2*2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/dtkzsyj586k9svw5c060epifny8zrbpl0n.png)
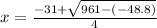
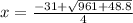
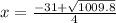
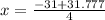
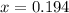
The second root will be found using the negative sign before the square root
:
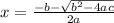
![x=\frac{-31-\sqrt{31^(2)-[4*2*(-6.1)]} }{2*2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/eore5ux7kvwkrk8qlqy7q88zxrcdqfoq6q.png)