Question

The solution set of


`(x ^(2) )/(x + 1) - 1 = (1)/(x + 1)`
is

A) {-1, 2}
B) {2}
C) {0, 1}
D) {1, -2}​

Answer 1

B) {2}

Explanation:

Subtracting the right side, we get ...

`(x^2)/(x+1)-1-(1)/(x+1)=0\\\\(x^2-x-1-1)/(x+1)=0\\\\((x-2)(x+1))/(x+1)=0\\\\x-2=0 \qquad\text{cancel like terms}\\\\x=2`

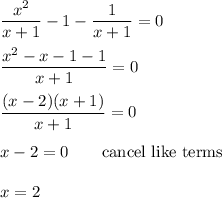
The quadratic has solutions x={-1, 2}, but x=-1 makes the original equation undefined. It is extraneous. The only valid solution is x = 2.

_____

Comment on this solution method

Often, subtracting one side of a rational equation so you get an equation of the form ( )/( ) = 0 will let you cancel common factors from numerator and denominator. This can help avoid any extraneous solutions. (You may still get an extraneous solution if a denominator factor appears at a higher power in the numerator. x³/x² = 0 reduces to x=0, but that is still extraneous.)