Question

The left end of a long glass rod 9.00 cm in diameter, with an index of refraction 1.55, is ground and polished to a convex hemispherical surface with a radius of 4.50 cm . An object in the form of an arrow 1.50 mm tall, at right angles to the axis of the rod, is located on the axis 23.0 cm to the left of the vertex of the convex surface.

Part A:Find the position of the image of the arrow formed by paraxial raysincident on the convex surface.Part B:Find the height of the image formed by paraxial rays incident onthe convex surface.

Answer 1

The position of the image and the height of the image are 19.68 cm and 0.828 mm.

Step-by-step explanation:

Given that,

Diameter = 9.00 cm

Index of refraction n₂= 1.55

Radius of curvature R= 4.50

Height of object h₀= 1.50 mm

Object distance u= 23.0 cm

(A). We need to calculate the image distance

Using formula for image of distance

`(n_(1))/(u)+(n_(2))/(v)=(n_(2)-n_(1))/(R)`

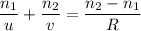
Put the value into the formula

`(1)/(23.0)+(1.55)/(v)=(1.55-1)/(4.50)`

`(1.55)/(v)=(1.55-1)/(4.50)-(1)/(23.0)`

`(1.55)/(v)=(163)/(2070)`

`v=(1.55*2070)/(163)`

`v=19.68\ cm`

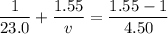
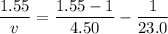
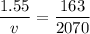
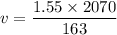
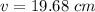
(B). We need to calculate the height of the image

Using formula of magnification

`m=(h_(i))/(h_(o))`

`(h_(i))/(h_(o))=(n_(1)d_(1))/(n_(2)d_(o))`

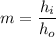
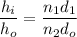
Put the value into the formula

`(h_(i))/(1.50)=(1*19.68)/(1.55*23.0)`

`h_(i)=(1*19.68*1.50)/(1.55*23.0)`

`h_(i)=0.828\ mm`

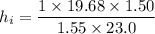
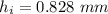
Hence, The position of the image and the height of the image are 19.68 cm and 0.828 mm.