Question

Define friction. Prove that tangent of angle of friction is equal to coefficient
of friction. ​

Answer 1

Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. the expression for friction, we get
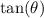`\(\tan(\theta)` = \mu. Therefore, the tangent of the angle of friction is indeed equal to the coefficient of friction.

It arises due to microscopic irregularities on the surfaces, causing resistance to motion.

The coefficient of friction quantifies this interaction, representing the ratio of the force of friction to the normal force between the surfaces.

To prove that the tangent of the angle of friction
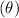`(\(\theta\))` is equal to the coefficient of friction (\mu), consider a body on the verge of sliding.

The force of friction
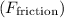`(\(F_{\text{friction}}\))` is given by
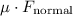`\(\mu \cdot F_{\text{normal}}\)`, where
`\(F_{\text{normal}}\)`is the normal force.

The tangent of the angle of friction is
`\(\tan(\theta) = \frac{F_{\text{friction}}}{F_{\text{normal}}}\).`

Substituting the expression for friction, we get
`\(\tan(\theta) = \mu\).`

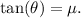
Therefore, the tangent of the angle of friction is indeed equal to the coefficient of friction.

This relationship is fundamental in understanding and calculating frictional forces in various physical scenarios.

Answer 2

Explained below

Step-by-step explanation:

- Friction is the force that opposes the motion between two or more objects/surfaces in contact with each other.

- On an inclined plane, the coefficient of static friction is given by the relation;

μ = F_max/F_n

Where;

F_max is maximum frictional force before slip = mg sin θ

F_n is normal force = mg cos θ

Thus;

μ = mg sin θ/mg cos θ

μ = tan θ