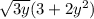Answer : The correct option is, (C)
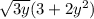
Step-by-step explanation :
The given expression is:
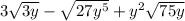
First we have to break into factors.

Now we have to make the power in even numbers.

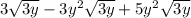
Now we have to take common
 from the given expression, we get:
from the given expression, we get:

Now we have to add like terms, we get:
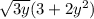
Therefore, the correct option is, (C)