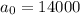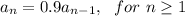Question

The native bird population in a city is decreasing at a rate of 10% per year due to industrialization of the area by humans. The population of native birds was 14,000 before the decrease began.

Complete the recursively-defined function to describe this situation.

Answer 1

`a_0 = 14000`

`a_(n) = 0.9a_(n - 1),~~ for ~n \ge 1`

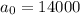
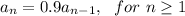
Explanation:

Let "a" represent the population.

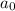`a_0` is the initial population.

`a_n` is the population at year n.

Since the population decreases 10% each year, that means that each year, the population is 90% of the previous year.

The initial population is 14,000.

Each year fater than, the population is 90% of the population of the previous year, or 0.9 time the population of the previous year.

`a_0 = 14000`

`a_(n) = 0.9a_(n - 1), ~~for ~n \ge 1`