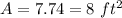Answer:
8 ft2
Explanation:
we know that
The diameter of the largest possible circle is equal to the length side of the square
The approximate area of the remaining board is equal to the area of the square minus the area of the circle
so
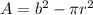
we have
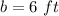 ------> length side of the square
------> length side of the square
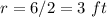 -----> the radius is half the diameter
-----> the radius is half the diameter
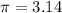
substitute the values
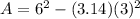
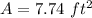
Round to the nearest whole number