Question

1. While solutions to the general quintic equation in terms of radicals are impossible to obtain, they do exist. Prove that the given quintic equation has real solutions. x^5-3x+1=0

Answer 1

Answer with step-by-step explanation:

Quintic function :It is defined as the function of degree five.

It can be defined
`ax^5+bx^4+cx^3+dx^2+ex+f=0`

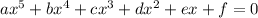
Where
`a\\eq0`,b,c,d,e and f are members of field , typically rational numbers,real numbers and complex numbers .

We are given that quintic equation

`x^5-3x+1=0`

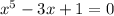
We have to prove that given quintic equation has real solutions

Using Discarte's rule

`f(x)=x^5-3x+1`

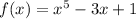
When are going from coefficient of first term to coefficient of second term then sign change and when we are going from coefficient of second term to coefficient of third term then sigh also changes .Therefore,, there are two times sign change .Hence, possible positive real roots are 2 or zero.Then number of positive real roots are even in number .

`f(-x)=-x^5+3x+1`

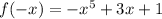
When we are going from first term to second term then sign change and then from second term to third term then sign does not changes.

Hence, possible negative real root is 1.

Therefore, we can say given quintic equation has real root.

Hence, proved

Answer 2

Explanation:

Given is a function as
`x^5-3x+1`

Equating to 0 we have equation

If the function f(x) has x intercepts then the solutions are real

Let us use remainder theorem and change of signs rule

f(0) = 1>0

f(-1) = -1+3+1=3

f(-2) = -32+6+1<0

This implies there is a real root between -1 and -2.

f(1) = -1

Since f(0) and f(1) have different signs, there exists a real root between 0 and 1.

f(2) = 32-6+1>0

Since f(1) and f(2) have different signs there exists a real root between 1 and 2.

Thus there are definitely three real solutions as

one between -1 and 0, one between 0 and 1, and third between 1 and 2.