Question

PLEASE HELP ME!!!!

What are the discontinuity and zero of the function f(x) =x^2+6x+8 over x+4

A)Discontinuity at (4, 6), zero at (−2, 0)
B)Discontinuity at (4, 6), zero at (2, 0)
C)Discontinuity at (−4, −2), zero at (−2, 0)
D)Discontinuity at (−4, −2), zero at (2, 0)

Answer 1

This is what I got, but you might want to double check me because I'm not that good at math (this is what I got for the discontinuity);

1. f(x)= x^2+6+8/x+4

*x+4=0

-4 -4

x= -4

This means that x cannot equal -4

2. f(x)= (x+2)(x-4)/(x+2)(x+2)

*Note: When I did my calculations, I cancelled out all (x+2) binomials except for one in the denominator*

f(x)= x-4/x+2

*x+2=0

-2 -2

x= -2

This means x cannot equal -2

*You may want to check my work, but I believe that your answer is going to be either C or D. Personally, I assume it's C, but that's just me. Anyway, it's probably going to be C or D, or at least that's what I think.*

Answer 2

Answer: Option C

Discontinuity at (−4, −2), zero at (−2, 0)

Explanation:

We have the following expression:

`f(x)=(x^2+6x +8)/(x+4)`

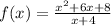
Note that the function is not defined for x = -4, since the division by zero is not defined

We factor the expression of the numerator.

We look for two numbers that when you multiply them you obtain as a result 8, and by adding both numbers you get as a result 6.

You can check that the numbers that meet these requirements are 4 and 2.

So the factors of the quadratic function are:

`(x + 4) (x + 2)`

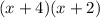
So
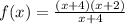`f(x) =((x+4)(x+2))/(x+4)` with
`x\\eq -4`

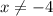
By simplifying the expression we have:

`f(x) =x+2` with
`x\\eq -4`

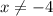
Since the function is not defined for x = -4 then f(x) has a discontinuity at the point (-4, -2)

To find the zero of the function you must equal f (x) to zero and solve for x

`f(x) =x+2=0`

`x+2-2=-2`

`x=-2`

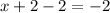
The zero of the function is: (-2, 0)

The answer is the Option C