Question

A water main pipe of diameter 10 cm enters a house 2 m below ground. A smaller diameter pipe carries water to a faucet 5 m above ground, on the second floor. Water flows at 2 ms1 in the main pipe and at 7 ms on the second floor. Find the diameter of the smaller diameter pipe. (i) [4 marks (ii) If the gauge pressure in the main pipe is 2x10 Pa, find the gauge pressure in the pipe on 15 marks) (ii) Discuss if it is possible to carry water to a faucet 17 m above ground, on the roof-top by 15 marks the second floor. extending the smaller diameter pipe

Answer 1

Step-by-step explanation:

Given that,

Diameter = 10 cm

Distance = 2 m

Speed
`v_(1)= 2\ m/s`

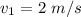
Speed
`v_(2)=7\ m/s`

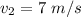
Pressure in main pipe
`P_(1)=2*10^(5)\ Pa`

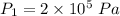
(I). We need to calculate the diameter

Using equation of continuity

`Av_(1)=Av_(2)`

`\pi((d_(1))/(2))^2* v_(1)=\pi((d_(2))/(2))^2* v_(2)`

`((10)/(2))^2*2=((d_(2))/(2))^2*7`

`d_(2)=\sqrt{(25*2*4)/(7)}`

`d_(2)=5.345\ cm`

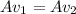
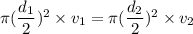
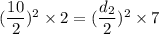
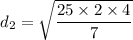
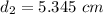
(II). We need to calculate the pressure the gauge pressure

Using Bernoulli equation

`P_(1)+(1)/(2)\rho v_(1)^2+\rho gh_(1)=P_(2)+(1)/(2)\rho v_(2)^2+\rho g h_(2)`

`P_(2)=P_(1)+(1)/(2)\rho(v_(1)^2-v_(2)^2)-\rho g(h_(1)-h_(2))`

`P_(2)=2*10^(5)+(1)/(2)*1000(4-49)-1000* 9.8*(5)`

`P_(2)=1.28500*10^(5)\ Pa`

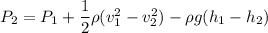
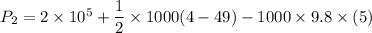
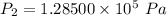
(III). If it is possible to carry water to a faucet 17 m above ground,

Using Bernoulli equation

`P_(1)+(1)/(2)\rho v_(1)^2+\rho gh=P_(3)+(1)/(2)\rho v_(3)^2+\rho g h_(3)`

`P_(3)=P_(1)+(1)/(2)\rho v_(1)^2-\rho g(h_(1)-h_(3))`

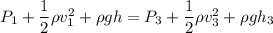
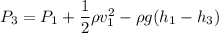
Here,
`h_(3)=0`

Put the value in the equation

`P_(3)=2*10^(5)+(1)/(2)*1000*4-1000* 9.8*17`

`P_(3)=3.5400*10^(5)\ Pa`

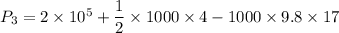
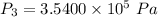
Hence, This is required solution.