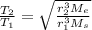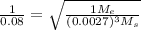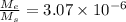Question

The Moon requires about 1 month (0.08 year) to orbit Earth. Its distance from us is about 400,000 km (0.0027 AU). Use Kepler’s third law, as modified by Newton, to calculate the mass of Earth relative to the Sun.

Answer 1

`(M_e)/(M_s) = 3.07 * 10^(-6)`

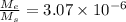
Step-by-step explanation:

As per Kepler's III law we know that time period of revolution of satellite or planet is given by the formula

`T = 2\pi \sqrt{(r^3)/(GM)}`

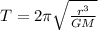
now for the time period of moon around the earth we can say

`T_1 = 2\pi\sqrt{(r_1^3)/(GM_e)}`

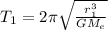
here we know that

`T_1 = 0.08 year`

`r_1 = 0.0027 AU`

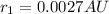
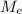`M_e` = mass of earth

Now if the same formula is used for revolution of Earth around the sun

`T_2 = 2\pi\sqrt{(r_2^3)/(GM_s)}`

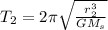
here we know that

`r_2 = 1 AU`

`T_2 = 1 year`

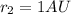
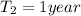
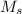`M_s` = mass of Sun

now we have

`(T_2)/(T_1) = \sqrt{(r_2^3 M_e)/(r_1^3 M_s)}`

`(1)/(0.08) = \sqrt{(1 M_e)/((0.0027)^3M_s)}`

`12.5 = \sqrt{(5.08 * 10^7)(M_e)/(M_s)}`

`(M_e)/(M_s) = 3.07 * 10^(-6)`