Question

Ciara is swinging a 0.015 kg ball tied to a string around her head in a flat, horizontal circle. The radius of the circle is 0.50 m. It takes the ball 0.70 seconds to complete one full circle. Calculate the tension in the string and its direction that provides the centripetal force acting on the ball to keep it in the circular path.

Answer 1

0.60 N, towards the centre of the circle

Step-by-step explanation:

The tension in the string acts as centripetal force to keep the ball in uniform circular motion. So we can write:

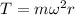`T=m\omega^2 r` (1)

where

T is the tension

m = 0.015 kg is the mass of the ball

`\omega` is the angular speed

r = 0.50 m is the radius of the circle

We know that the period of the ball is T = 0.70 s, so we can find the angular speed:

`\omega=(2\pi)/(T)=(2\pi)/(0.70 s)=8.98 rad/s`

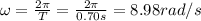
And by substituting into (1), we find the tension in the string:

`T=(0.015 kg)(8.98 rad/s)^2(0.50 m)=0.60 N`

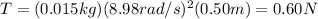
And in an uniform circular motion, the centripetal force always points towards the centre of the circle, so in this case the tension points towards the centre of the circle.