Answer:
57.5%
Explanation:
We know that the total number of the population is made up of 15% x's and 85% of y's and let the total amount of population be z:
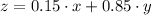
we also know that x's are twice as likely to commit crimes than y's:
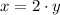
Therefore is we can solve for x by substituting y=x/2 into the first equation:
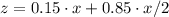
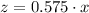
Therefore the chances of the x's committing the crime is 57.5% of the x's are likely to commit the crime.