Question

Determine if triangle ABC with coordinates A (0, 2), B (2, 5), and C (−1, 7) is an isosceles triangle. Use evidence to support your claim. If it is not an isosceles triangle, what changes can be made to make it isosceles? Be specific.

Answer 1

The triangle ABC is an isosceles right triangle

Explanation:

we have

The coordinates of triangle ABC are

A (0, 2), B (2, 5), and C (−1, 7)

we know that

An isosceles triangle has two equal sides and two equal internal angles

The formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

step 1

Find the distance AB

substitute in the formula

`d=\sqrt{(5-2)^(2)+(2-0)^(2)}`

`d=\sqrt{(3)^(2)+(2)^(2)}`

`dAB=√(13)\ units`

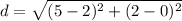
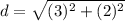
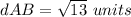
step 2

Find the distance BC

substitute in the formula

`d=\sqrt{(7-5)^(2)+(-1-2)^(2)}`

`d=\sqrt{(2)^(2)+(-3)^(2)}`

`dBC=√(13)\ units`

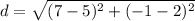
step 3

Find the distance AC

substitute in the formula

`d=\sqrt{(7-2)^(2)+(-1-0)^(2)}`

`d=\sqrt{(5)^(2)+(-1)^(2)}`

`dAC=√(26)\ units`

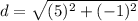
step 4

Compare the length sides

`dAB=√(13)\ units`

`dBC=√(13)\ units`

`dAC=√(26)\ units`

`dAB=dBC`

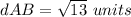
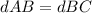
therefore

Is an isosceles triangle

Applying the Pythagoras Theorem

`(AC)^(2) =(AB)^(2)+(BC)^(2)`

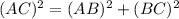
substitute

`(√(26))^(2) =(√(13))^(2)+(√(13))^(2)`

`26=13+13`

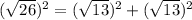
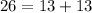
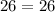`26=26` -----> is true

therefore

Is an isosceles right triangle