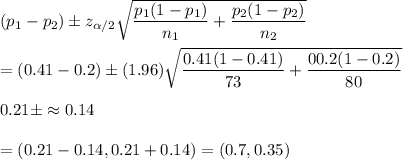Answer: There is a significant difference in the proportions.
The 95% confidence interval for the difference of the two proportions.(0.7,0.35)
Explanation:
Given : In San Jose a sample of 73 mail carriers showed that 30 had been bitten by an animal during one week.
So the proportion of mail carriers had been bitten by an animal during one week:
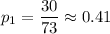
In San Francisco in a sample of 80 mail carriers, 16 had received animal bites.
The proportion of mail carriers had been bitten by an animal during one week in San Francisco:
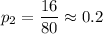
Since ,
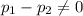 , there is a significant difference in the proportions
, there is a significant difference in the proportions
The confidence interval for population proportion is given by :-