Question

In triangle abc, angle A is the right angle. What is the value of y?

Answer 1

7sinΠ/6 (A)

Explanation:

Since the triangle given is a right angled triangle, the SOH CAH TOA method will be employed.

Given opposite side to be 'y' (the side facing the acute angle)

The hypotenuse = 7feet(the longest side)

Any the angle theta = 30°

According to SOH;

sin(theta) = opposite/Hypotenuse

Sin30° = y/7

y = 7sin30°

Note that 180°=Πrad

30° = Π/6rad

y = 7sinΠ/6 (A)

Answer 2

A

Explanation:

In a right triangle, the side opposite to the 90 degree angle (here, side opposite to angle A) is known as the hypotenuse.

Also, the side that is "opposite" to the angle given (here side opposite is y to angle given 30 degrees) is the opposite side.

Since we want to find "opposite" and have "hypotenuse" , recalling trig ratios, we can say opposite/hypotenuse is the ratio SINE, so we can write:

`Sin(30)=(y)/(7)`

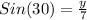
We solve for y:

`Sin(30)=(y)/(7)\\y = 7 Sin(30)`

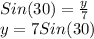
Since the answer choice has angles in radians, we recall 30 degrees is
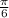`(\pi)/(6)` radians.

Thus, the correct answer is
`7Sin((\pi)/(6))`, or option A