Question

How do I solve a word problem using a matrice with these equations:

10x+12y+20z=1240
1.5x+2y+4z=240
1x+1y+1z=70

Answer 1

In matrix form, the system

`\begin{cases}10x+12y+20z=1240\\1.5x+2y+4z=240\\x+y+z=70\end{cases}`

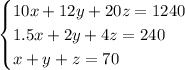
is

`\begin{bmatrix}10&12&20\\1.5&2&4\\1&1&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}1240\\240\\70\end{bmatrix}`

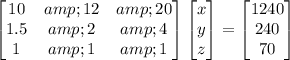
Multiplying through both sides of the second equation by 2 doesn't change the system fundamentally:

`\begin{bmatrix}10&12&20\\3&4&8\\1&1&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}1240\\480\\70\end{bmatrix}`

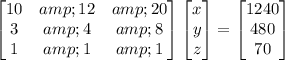
Then we can try to find a solution via elimination. Consider the augmented matrix,

`\left[\begin{array}c1&1&1&70\\10&12&20&1240\\3&4&8&480\end{array}\right]`

Subtract 10(row 1) from row 2, and subtract 3(row 1) from row 3:

`\left[\begin{array}c1&1&1&70\\0&2&10&540\\0&1&5&270\end{array}\right]`

Subtract 2(row 2) from row 3:

`\left[\begin{array}ccc1&1&1&70\\0&2&10&540\\0&0&0&0\end{array}\right]`

We end up with a row of 0s, which means the system is underdetermined and dependent, or that it has infinitely many solutions.