Question

Which of the following is equal to the square root of the cube root of 5?

5 to the power of one third
5 to the power of one sixth
5 to the power of two thirds
5 to the power of three halves

Answer 1

5 to the power of one sixth

Explanation:

`\sqrt[2]{\sqrt[3]{5}}\\(5^{(1)/(3)})^{(1)/(2)}\\5^{(1)/(6)}`

Answer 2

First option: 5 to the power of one sixth (
`5^{(1)/(6)}`)

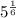Explanation:

It is important to remember the following:

`\sqrt[n]{\sqrt[m]{a} }=\sqrt[nm]{a}`

`\sqrt[n]{a}=a^{(1)/(n)`

In this case, given:

`\sqrt[2]{\sqrt[3]{5} }`

You can identify that:

`n=2` and
`m=3`

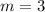
Therefore, knowing this, you can conclude that:

`=\sqrt[2*3]{5}=\sqrt[6]{5}=5^{(1)/(6)}`

You can observe that this answer matches with the second option.