Question

Suppose you take out a loan for $9,000, at 12% ordinary interest. If the amount of interest is $762.00, what is the time period? (Round any fraction to the next higher day) a. 254 days b. 246 days c. 258 days d. 250 days

Answer 1

Option b - 246 days.

Explanation:

Given : Suppose you take out a loan for $9,000, at 12% ordinary interest. If the amount of interest is $762.00.

To find : What is the time period?

Solution :

We are going to apply interest formula which is given as,

`A=P(1+r)^t`

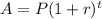
Where, I is the amount of interest I=$762

P is the principal value P=$9000

r is the interest rate r=12%=0.12

t is the time period

Amount is A=P+I=9000+762=$9762

Substitute the value in the formula,

`9762=9000(1+0.12)^t`

`(9762)/(9000)=(1.12)^t`

`1.0846=(1.12)^t`

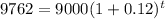
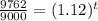
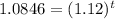
Taking log both side,

`\log(1.08)=t\log(1.12)`

`t=(\log(1.08))/(\log(1.12))`

`t=0.679`

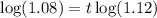
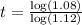
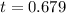
Converting time from year into days,

`t=0.679* 365\approx246`

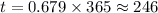
Therefore, Option b is correct.

Answer 2

answer is option c

Explanation:

Amount = $9,000

interest rate (r) = 12%

interest = $762.00

time = ?

we know,

`I = (PRT)/(100)`

`762  = \frac {9000* 12* T}{100}`

t = 0.7056 years

t = 0.7056 × 365 days

t = 257.54 days ≅ 258 days

correct answer is option c.