Question

The base of a solid in the region bounded by the parabola x2 + y = 4 and the line x + y = 2. Cross sections of the solid perpendicular to the x-axis are semicircles. What is the volume, in cubic units, of the solid?

Answer 1

the decimal answer in the above answer is correct, but the fraction is wrong. it's
`(81\pi )/(80\\)`

Answer 2

volume of the solid is 3.180

Explanation:

given data

line x + y = 2

parabola x2 + y = 4

to find out

the volume of the solid

solution

we draw a graph between line and parabola as show in fig given below attach

line cut at (-1,3) and (2,0)

so the length of diameter is ( 4 - x²) - (2 - x)

and radius of this semi circle will be ( 4 - x² - 2 + x ) /2

radius = (-x² + x + 2 ) /2

and r(x) will be = (-x² + x + 2 ) /2

and A(x) will be = π ( r(x)² ) /2

we will integrate from -1 to 2

=
`\int_(-1)^(2)A(x))`

=
`\int_(-1)^(2)(π ( (-x² + x + 2 ) /2)² ) /2))`

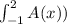
= 81π / 20

volume of the solid is 3.180