Question

Enter the values for the highlighted variables to complete the steps to find the sum: (see picture)

Answer 1

a = -1

b = -9

c = 9

d = 3

e = 3

f = 2

g = 3/2

Explanation:

* Lets explain how to solve the problem

∵
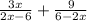`(3x)/(2x-6)+(9)/(6-2x)` are rational fractions

- To add or subtract the rational fractions they must have same

denominator

∵ 6 - 2x must be written 2x - 6, take (-1) as a common factor from 6 - 2x

∴ - 1(-6 + 2x) = - 1(2x - 6)

∴
`(3x)/(2x - 6)+(9)/(6-2x)=(3x)/(2x-6)+(9)/(-1(2x-6))`

∴ a = -1

∵ 9 ÷ -1 = -9

∴ =
`(3x)/(2x-6)+(-9)/(2x-6)`

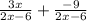
∴ b = -9

∵ The denominators of the two fractions are 2x - 6

∴ We can add them by adding their numerator

∵ 3x + -9 = 3x - 9

∴ =
`(3x-9)/(2x-6)`

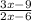
∴ c = 9

∵ 3x - 9 has a common factor 3

∴ 3x - 9 = 3(x - 3)

∵ 2x - 6 has common factor 2

∴ 2x - 6 = 2(x - 3)

∴ =
`(3(x-3))/(2(x-3))`

∴ d = 3 , e = 3 , f = 2

- The fraction has same factor (x - 3) up and down then we can cancel

them together

∴ =
`(3)/(2)`

∴ g = 3/2