Answer:
(g-f) (-1)= sqrt(15)
(f/g)(-1)= 0
(g+f)(2)=sqrt(3)-3
(g*f)(2)=-3*sqrt(3)
Explanation:
We have to eval the expressions given in the point indicated.
Lets start by the first equation
(g-f)(-1)= g(-1) - f(-1)=
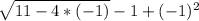 =
=
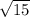
Now, lest continue with the others
(f/g)(-1)= f(-1)/g(-1)= (1-1)/sqrt(15)=0
(g+f)(2)=g(2)+f(2)=sqrt(3)-3
(g*f)(2)=g(2)*f(2)=sqrt(3)*(-3)=-3sqrt(3)