Answer:
Mass% Cr = 85.5%
Step-by-step explanation:
Given:
Mass of CrBr3 sample = 0.8409 g
Mass of the AgBr precipitate = 1.0638 g
To determine:
The mass percent of Cr in the sample
Calculation:
The reaction of CrBr3 with silver nitrate results in the precipitation of the bromide ion as silver chloride (AgBr) and Cr as soluble Cr(NO3)2
CrBr3(aq) + 3AgNO3(aq)→ 3AgBr(s) + Cr(NO3)3(aq)
Molecular weight of AgBr =187.77 g/mol
Moles of AgBr precipitated is:
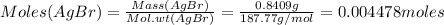
Since 1 mole of AgBr contains 1 mole of Cl, therefore:
# moles of Cl = 0.004478 moles
At wt of Cl = 35.45 g/mol
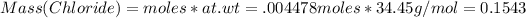
Mass%(Cr) = 100 - 14.50=85.5%