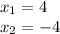2 Answers

Dounia · Answer 1 · 2020-05-01T03:14:09+0000

For this case we have two quadratic equations:

x ^ 2 = 25

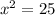
We apply square root to both sides of the equation:

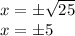
$x = \pm \sqrt {25}\\x = \pm5$

Thus, we have two solutions:

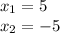
$x_ {1} = 5\\x_ {2} = - 5$

On the other hand we have:

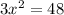
3x ^ 2 = 48

We divide by 3 on both sides of the equation:

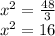
$x ^ 2 = \frac {48} {3}\\x ^ 2 = 16$

We apply square root to both sides of the equation:

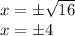
$x = \pm \sqrt {16}\\x = \pm4$

Thus, we have two solutions:

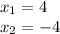
$x_ {1} = 4\\x_ {2} = - 4$

Answer:

Equation 1:

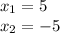
$x_ {1} = 5\\x_ {2} = - 5$

Equation 2:

$x_ {1} = 4\\x_ {2} = - 4$

Please log in or register to add a comment.