Answer: The final temperature of the mixture is 66°C
Step-by-step explanation:
When hot water is mixed with cold water, the amount of heat released by hot water will be equal to the amount of heat absorbed by cold water.
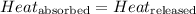
The equation used to calculate heat released or absorbed follows:
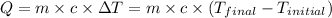
![m_1* c* (T_(final)-T_1)=-[m_2* c* (T_(final)-T_2)]](https://img.qammunity.org/2020/formulas/physics/college/jimhrvet2ab55e8azsefjq8pz22nqyihiz.png) ......(1)
......(1)
where,
q = heat absorbed or released
 = mass of hot water = 150.0 g
= mass of hot water = 150.0 g
 = mass of cold water = 100.0 g
= mass of cold water = 100.0 g
 = final temperature = ?°C
= final temperature = ?°C
 = initial temperature of hot water = 90.0°C
= initial temperature of hot water = 90.0°C
 = initial temperature of cold water = 30.0°C
= initial temperature of cold water = 30.0°C
c = specific heat of water= 4.186 J/g°C
Putting values in equation 1, we get:
![150* 4.186* (T_(final)-90)=-[100* 4.186* (T_(final)-30)]\\\\T_(final)=66^oC](https://img.qammunity.org/2020/formulas/chemistry/college/9icq6c2perpti8jid66nlke6soelynuaje.png)
Hence, the final temperature of the mixture is 66°C