Answer:
599/2
Explanation:

I'm going to use quotient rule which says:
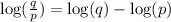 :
:
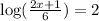
Now we are going write this in equivalent expontial form. That is,
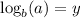 implies
implies
 .
.
Writing in exponetial form:


Multiply both sides by 6:
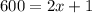
Subtract 1 on both sides:
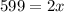
Divide both sides by 2:
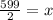
When it comes to logarithms, you should check your solution(s).

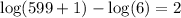
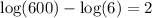
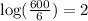
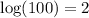
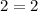
The solution checks out.