Question

Nernst Equation – For the following reaction:

Mn (s) + Cr3+ (aq) ? Mn2+ (aq) + Cr (s)

(a) Write the three balanced equations (each half-cell and the overall):

(b) What is the standard cell potential (E°cell) for this Mn/Cr cell?

(c) What will be the cell potential when [Mn2+] = 0.20 M and [Cr3+] = 1.0 × 10-4 M ?

(d) What will be the cell potential when [Mn2+] = 1.0 × 10-4 M and [Cr3+] = 0.20 M ?

Answer 1

For a: The reactions are written below.

For b: The standard cell potential of the given cell is +0.44 V.

For c: The cell potential for the given values is 0.408 V

For d: The cell potential for the given values is 0.4724 V.

Step-by-step explanation:

The given cell is:

`Mn(s)/Mn^(2+)||Cr^(3+)/Cr(s)`

• For a:

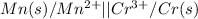
Half reactions for the given cell follows:

Oxidation half reaction:
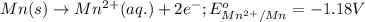`Mn(s)\rightarrow Mn^(2+)(aq.)+2e^-;E^o_(Mn^(2+)/Mn)=-1.18V` ( × 3)

Reduction half reaction:
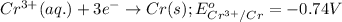`Cr^(3+)(aq.)+3e^-\rightarrow Cr(s);E^o_(Cr^(3+)/Cr)=-0.74V` ( × 2)

Net reaction:
`Mn(s)+Cr^(3+)(aq.)\rightarrow Mn^(2+)(aq.)+Cr(s)`

• For b:

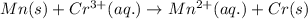
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.

To calculate the
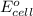`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

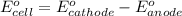
Putting values in above equation, we get:

`E^o_(cell)=-0.74-(-1.18)=0.44V`

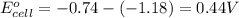
Hence, the standard cell potential of the given cell is 0.44 V

• For c:

To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Mn^(2+)])/([Cr^(3+)])`

where,

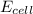`E_(cell)` = electrode potential of the cell = ?V

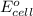`E^o_(cell)` = standard electrode potential of the cell = +0.44 V

n = number of electrons exchanged = 6

`[Cr^(3+)]=1.0* 10^(-4)M`

`[Mn^(2+)]=0.20M`

Putting values in above equation, we get:

`E_(cell)=0.44-(0.059)/(6)* \log((0.20)/(1.0* 10^(-4)))\\\\E_(cell)=0.408V`

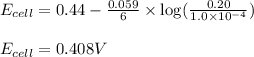
Hence, the EMF of the cell for the given concentration is 0.408 V.

• For d:

To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Mn^(2+)])/([Cr^(3+)])`

where,

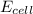`E_(cell)` = electrode potential of the cell = ?V

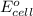`E^o_(cell)` = standard electrode potential of the cell = +0.44 V

n = number of electrons exchanged = 6

`[Cr^(3+)]=0.20M`

`[Mn^(2+)]=1.0* 10^(-4)M`

Putting values in above equation, we get:

`E_(cell)=0.44-(0.059)/(6)* \log((1.0* 10^(-4))/(0.20))\\\\E_(cell)=0.4724V`

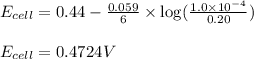
Hence, the EMF of the cell for the given concentration is 0.4724 V.