Answer:
The pilot has to fly the plane at an angle 83° north of west.
Step-by-step explanation:
The airspeed of an airplane is 600 km/hr ( north direction)
In figure,
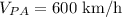
A wind blowing northeast at 90 km/h
In figure,
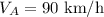
Let actual speed of airplane and direction of plane,
Speed = x km/h
Direction = Ф (north of west, refer figure)
Now, we divide each velocity in horizontal and vertical component.
- For wind,
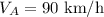
Horizontal component,
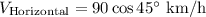
Vertical component,
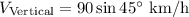
Horizontal component,
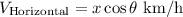
Vertical component,
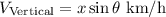
If the airplane needs to head due north.
Horizontal component must be cancel out.
Therefore,
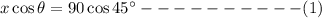
Speed of airplane is 600 km/h due to north.
So, Sum of vertical component must be equal to 600
Therefore,

Using eq(1) and eq(2) we get,
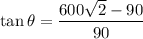
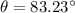
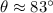
Hence, The pilot has to fly the plane at an angle 83° north of west.