Question

Consider the following recursively defined sequence a1 = 2 an = an-1 – 3 for n >= 2 In this question, we will prove that an = -3n + 5 for all n >=1. Fill the blanks

Let P(n) = __________. We prove that for all n there exists Z, if n>=0

Base case: The base case is n = _________

Proof of the base case: ____________

Induction step: The induction hypothesis is ___ _________

Our goal in the induction is to prove ________ ________

Proof of the induction step:

Answer 1

Answer with Step-by-step explanation:

We are given that

`a_1=2`

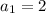
`a_n=a_(n-1)-3` for
`for  [tex]n\geq2`

We have to prove that
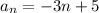`a_n=-3n+5` for all n equal and greater than 1

proof: Let P(n)=
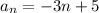`a_n=-3n+5` for all n equals to and greater than 1

We prove that for all n there exists Z,if n greater and equals to zero

Base case : The base case is n=1

Substitute n=1 then we get

P(1)=-3(1)+5=2

This is true for n=1

Induction step : suppose that P(n) is true for n=k where k greater than 1

Then P(k)=-3k+5

Now, we shall prove that for n=k+1, P(n) is true for n=k+1

P(k+1)=-3(k+1)+5

P(k+1)=-3k-3+5=-3k+5-3

`P(k+1)=a_k-3`

`a_(k+1)=a_k-3`

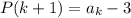
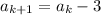
We are given that
`a_n=a_(n-1)-3` for n equal to and greater than 2

Therefore, P(n) is true for n=k+1

Hence, P(n)=-3n+5 for all n equal and greater than 1