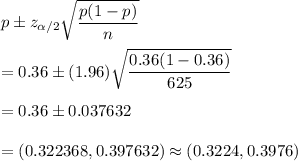Answer: (0.3224,0.3976)
Explanation:
Given : Sample size : n=625
Number of people check their work email when they are at home =225
The probability of people check their work email when they are at home :
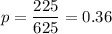
Significance level :
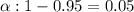
Critical value :
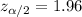
The confidence interval for population proportion is given by :-